


Next: Anisotropy energy
Up: Micromagnetic description
Previous: Micromagnetic description
Contents
Taking the atomic representation for exchange energy between two
moments (equation 2.2), we can assume that the angle
between two neighbouring spins is
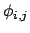 . The sum of all the
exchange energies based on equation 2.4 can be rewritten as:
. The sum of all the
exchange energies based on equation 2.4 can be rewritten as:
where 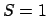 since
since
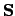 is a unit vector (equation 2.3) and for small values of
is a unit vector (equation 2.3) and for small values of
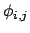 we use the leading terms in the Taylor expansion of
we use the leading terms in the Taylor expansion of
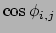 (figure 2.6):
(figure 2.6):
With this assumption, equation 2.18 can be rewritten:
where
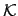 is a constant. Since
is a constant. Since
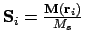 and
and
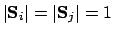 (figure 2.5):
(figure 2.5):
and
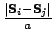 approximates the spatial
derivative of
approximates the spatial
derivative of
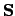 over the lattice spacing
over the lattice spacing 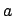 .
.
If we take
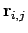 to be a lattice translation vector of magnitude
to be a lattice translation vector of magnitude 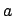 as in
figure 2.5, the directional derivative
as in
figure 2.5, the directional derivative
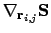 can be used
to express
can be used
to express
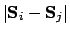 .
.
Inserting this into equation 2.18, the exchange energy can
now be represented as (Blundell, 2001):
if we take
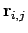 outside the summations and redefine this
as
outside the summations and redefine this
as 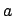 (the nearest neighbour distance). Since we will integrate over
volume to obtain the continuous representation, if we consider a unit
cell site number
(the nearest neighbour distance). Since we will integrate over
volume to obtain the continuous representation, if we consider a unit
cell site number 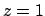 ,
, 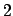 or
or 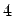 (for simple cubic, body-centred
cubic and face-centred cubic respectively), we can define the exchange
coupling constant (Aharoni, 2000):
(for simple cubic, body-centred
cubic and face-centred cubic respectively), we can define the exchange
coupling constant (Aharoni, 2000):
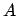 The exchange coupling constant
The exchange coupling constant
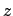 The cell site number;
The cell site number; 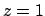 ,
, 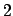 or
or 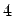 for simple cubic, body-centred
cubic and face-centred cubic respectively
for simple cubic, body-centred
cubic and face-centred cubic respectively
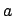 The distance between nearest neighbours in a crystalline lattice
The distance between nearest neighbours in a crystalline lattice
We can now ignore the discrete lattice, yielding the continuous form:
Figure:
The functions
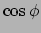 (solid black) and
(solid black) and
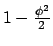 (dashed red). The dotted green line represents the difference between the two functions
(dashed red). The dotted green line represents the difference between the two functions
|
|



Next: Anisotropy energy
Up: Micromagnetic description
Previous: Micromagnetic description
Contents
Richard Boardman
2006-11-28
![]() . The sum of all the
exchange energies based on equation 2.4 can be rewritten as:
. The sum of all the
exchange energies based on equation 2.4 can be rewritten as:
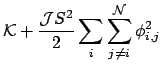
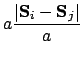
![]() to be a lattice translation vector of magnitude
to be a lattice translation vector of magnitude ![]() as in
figure 2.5, the directional derivative
as in
figure 2.5, the directional derivative
![]() can be used
to express
can be used
to express
![]() .
.
![$\displaystyle - \mathcal{J}S^2 \sum_i \sum_{j\neq i}^{\mathcal{N}} \left [ (\ensuremath{\mathbf{r}}_{i,j} \cdot \nabla)\ensuremath{\mathbf{S}} \right ] ^2$](img136.png)
![$\displaystyle - \mathcal{J}S^2a^2 \sum_i \sum_{j\neq i}^{\mathcal{N}} \left [(\nabla m_x)^2 + (\nabla m_y)^2 + (\nabla m_z)^2 \right ]$](img137.png)
![\includegraphics[width=1.0\textwidth,clip]{images/smallcos}](img145.png)