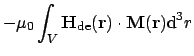 |
(2.29) |
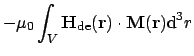 |
(2.29) |
where
![]() is the
demagnetising field with components contributed from the
divergence of magnetisation within the volume and surface poles (O'Handley, 1999):
is the
demagnetising field with components contributed from the
divergence of magnetisation within the volume and surface poles (O'Handley, 1999):
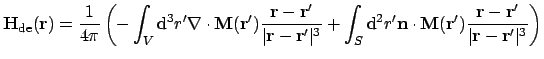 |
(2.30) |
![]() The demagnetising field in a system
The demagnetising field in a system
![]() In magnetostatics, the vector normal to the surface of a sample
In magnetostatics, the vector normal to the surface of a sample
and
![]() is the surface normal.
is the surface normal.
A complete derivation of
![]() is given
in Brown (1963), Aharoni (2000) and Blundell (2001).
is given
in Brown (1963), Aharoni (2000) and Blundell (2001).