


Next: Parameters of the antidot
Up: Introduction
Previous: Introduction
Contents
For a hexagonal lattice with base vectors:
the lattice points are:
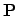 The positional vector for lattice geometries
Shown in figure 6.4 on the right is a hexagonal structure
which exhibits this property. However, one should note that there are
two ways of packing this layer as there are two positions in which the
first sphere can be placed. The two structures are called
hexagonal close-packed and face-centred cubic. The
hexagonal close-packed structure, or hcp, has the third layer
in
The positional vector for lattice geometries
Shown in figure 6.4 on the right is a hexagonal structure
which exhibits this property. However, one should note that there are
two ways of packing this layer as there are two positions in which the
first sphere can be placed. The two structures are called
hexagonal close-packed and face-centred cubic. The
hexagonal close-packed structure, or hcp, has the third layer
in 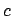 having the same
having the same 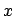 and
and 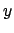 coordinates as the first layer, the
second layer has the same
coordinates as the first layer, the
second layer has the same 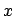 and
and 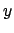 coordinates as the fourth layer
(ABABAB...) and so on (Kittel, 1996). The face-centred cubic
structure has an alternative arrangement of spheres in the third layer
where the spheres share the same
coordinates as the fourth layer
(ABABAB...) and so on (Kittel, 1996). The face-centred cubic
structure has an alternative arrangement of spheres in the third layer
where the spheres share the same 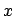 coordinate with the first layer
but have different
coordinate with the first layer
but have different 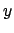 coordinates (ABCABC...). Although this
arrangement appears at the outset to be hexagonal, by rotating its
primitive cell the vectors can be shown to be a variant of a cubic
lattice.
coordinates (ABCABC...). Although this
arrangement appears at the outset to be hexagonal, by rotating its
primitive cell the vectors can be shown to be a variant of a cubic
lattice.
Figure 6.4:
Two layers of spheres packed cubically (left) and hexagonally (right)
|
|
Figure 6.5:
600x600x150nm cut of simple cubic nickel antispheres in zero applied field. The colouring represents the angle between 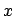 and
and 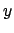 in radians; the lower left inset shows an
in radians; the lower left inset shows an 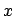 -
-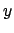 cut-plane through the centre of the sample, the lower right shows a cut-plane through a lower part of the same sample
cut-plane through the centre of the sample, the lower right shows a cut-plane through a lower part of the same sample
|
|



Next: Parameters of the antidot
Up: Introduction
Previous: Introduction
Contents
Richard Boardman
2006-11-28
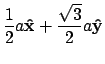
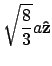
![\includegraphics[width=1.0\textwidth]{images/600x600x150-3das.eps}](img428.png)