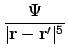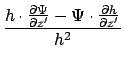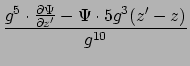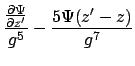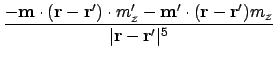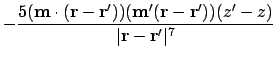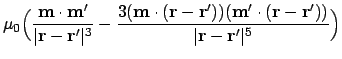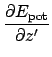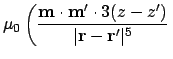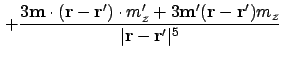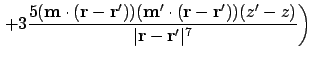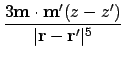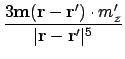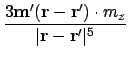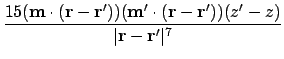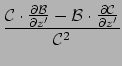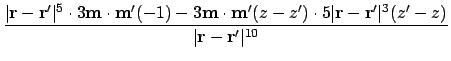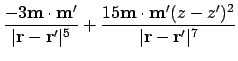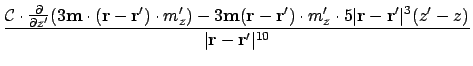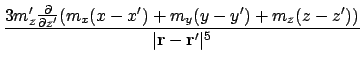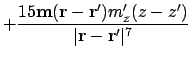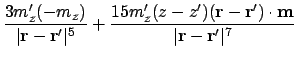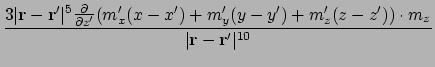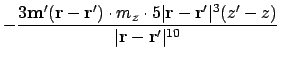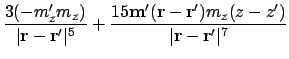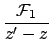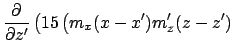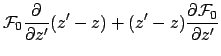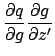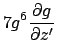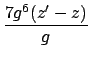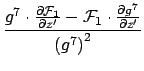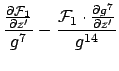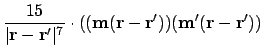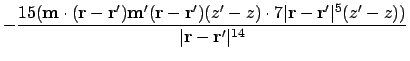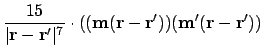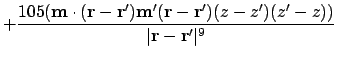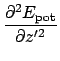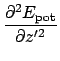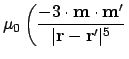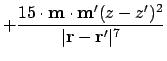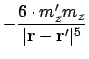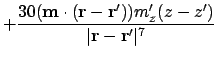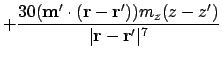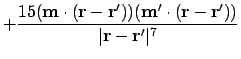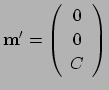


Next: Supporting equations for the
Up: thesis
Previous: Summary
Contents
Analytical calculation of the stray field
Since the phase shift of the cantilever attached to the sharp tip in a
magnetic force microscope (Sáenz et al., 1987) when measured corresponds
to the measured signal (McVitie et al., 2001), the second derivative of
the stray field (Rugar et al., 1990, Hug et al., 1998) is proportional to the rate
of change of the force on the tip (Barthelmeß et al., 2004).
If the second derivative is evaluated at a fixed height above a
demagnetising energy dataset of micromagnetic simulation results then
this is comparable to a magnetic force microscope. This derivative is
presented in this appendix.
The dipolar energy between two points in a magnetic system, assuming
each discrete cell is a dipole, can be considered to be
where
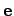 is the unit vector of
is the unit vector of
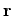 .
.
For fixed
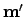 (such as that in the magnetic tip in magnetic
force microscopy), the effective field is
(such as that in the magnetic tip in magnetic
force microscopy), the effective field is
because
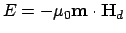 , noting that
, noting that
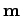 is
located at
is
located at
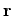 and
and
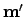 -- the tip -- is located at
-- the tip -- is located at
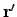 . We define:
. We define:
For the MFM data:
Expand A.1 by substituting A.3:
We precompute some expressions:
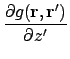 |
 |
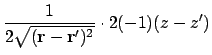 |
(A.9) |
| |
 |
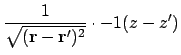 |
(A.10) |
| |
 |
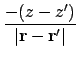 |
(A.11) |
| |
 |
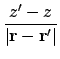 |
(A.12) |
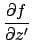 |
 |
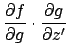 |
(A.15) |
| |
 |
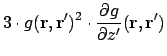 |
(A.16) |
| |
 |
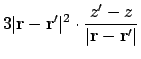 |
(A.17) |
| |
 |
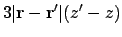 |
(A.18) |
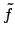 |
 |
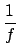 |
(A.19) |
| |
 |
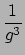 |
(A.20) |
| |
 |
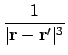 |
(A.21) |
| |
 |
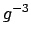 |
(A.22) |
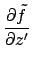 |
 |
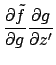 |
(A.23) |
| |
 |
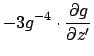 |
(A.24) |
| |
 |
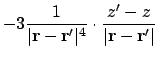 |
(A.25) |
| |
 |
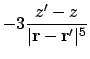 |
(A.26) |
so
so
Looking at the mixed terms in A.5:
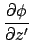 |
 |
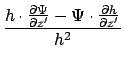 |
(A.40) |
| |
 |
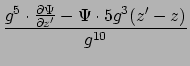 |
(A.41) |
| |
 |
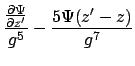 |
(A.42) |
| |
 |
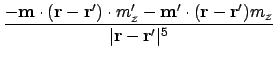 |
|
| |
|
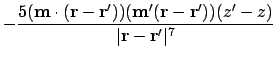 |
(A.43) |
Combining the above to give the first derivative of the dipolar interaction energy as A.5:
With respect to 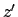 :
:
To find
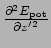 , we need the derivatives
of
, we need the derivatives
of
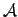 ,
,
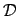 ,
,
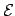 and
and
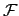 :
:
In the derivative, only the terms with 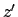 matter:
matter:
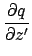 |
 |
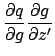 |
(A.72) |
| |
 |
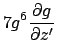 |
(A.73) |
| |
 |
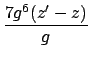 |
(A.74) |
| |
 |
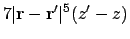 |
(A.75) |
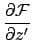 |
 |
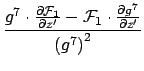 |
(A.76) |
| |
 |
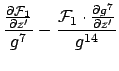 |
(A.77) |
| |
 |
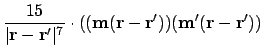 |
|
| |
|
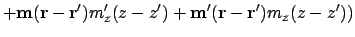 |
|
| |
|
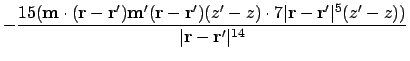 |
(A.78) |
| |
 |
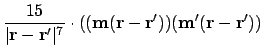 |
|
| |
|
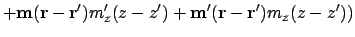 |
|
| |
|
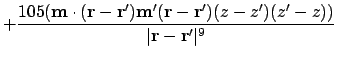 |
(A.79) |
The second derivative is:
Where possible, collecting terms and expanding gives:
This is the final second derivative, which should be proportional to the signal at the tip of the MFM -- assuming the MFM tip is a dipole:
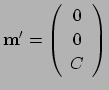 |
(A.82) |



Next: Supporting equations for the
Up: thesis
Previous: Summary
Contents
Richard Boardman
2006-11-28
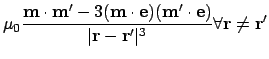
![]() (such as that in the magnetic tip in magnetic
force microscopy), the effective field is
(such as that in the magnetic tip in magnetic
force microscopy), the effective field is
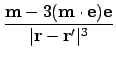
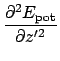
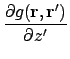
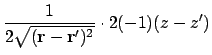
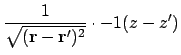
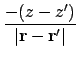
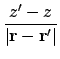
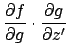
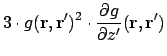
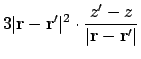
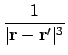
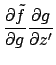
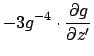
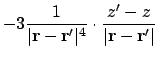
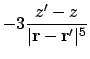
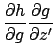
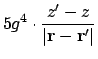
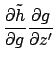
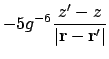
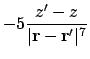
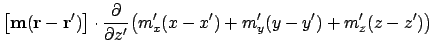
![$\displaystyle + \bigl[\ensuremath{\mathbf{m}}'(\ensuremath{\mathbf{r}}-\ensurem...
...igr]\cdot {\partial \over \partial z'}\bigl(m_x(x-x')+m_y(y-y')+m_z(z-z')\bigr)$](img548.png)