Decision Making Under Uncertainty
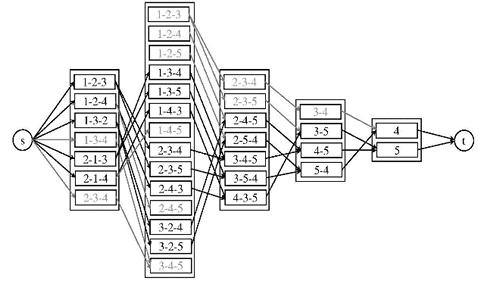
Our work includes developing and/or investigating new mathematical models which capture the uncertainty and other features such as competition, equilibrium and hierarchical relationships between decision makers. Typical examples are stochastic principal agent models (Stackelberg leader follower models), stochastic Nash equilibrium models, stochastic bilevel programming models, stochastic mathematical programs with equilibrium constraints (SMPEC) models and stochastic equilibrium programs with equilibrium constraints (SEPEC) models.