Image Compression Basics

by Kirk Martinez

Variety of algorithms

As this is a continuously progressing field there are many evolving techniques. The common theme is to make use of statistical redundancy in the image data or cause loss only in areas which are less noticed by the eye. Properties of vision are thus very important! Especially masking - where small errors can be hidden near a striking feature like an edge.
 

Statistical Algorithms

Simply applying ZIP or similar compression will not work that well as the histogram of image values is usually quite spread. However images of paper and text for example compress quite well.
The following image from the Alan Turing archive starts out as 2.56MB:

Compresses to 1.71MB after putting the uncompressed TIFF file into a ZIP file.
Its histogram looks like this:

It is clearly peaked - which helps! - basically the common values will be stored with a code using fewer bits than the less frequent values.

A lossless technique where no actual degradation occurs can only achieve around 3:1 compression with non-document
images, but is ideal for archiving where no loss can be tolerated. Documents containing text with large uniform areas can be
compressed such as run-length coding where the number of consecutive identical values are stored instead. A technique which is
very useful for text or data with a concentration of some values (a peaked histogram) is Huffman coding. For example some data
may have mostly values of 50 with decreasing amounts of values either side. Huffman coding assignes a short code to the value 50,
a slightly longer one to 49 and 51, and so on. In practice all the values are arranged in order of probability and assigned longer
codes. Clearly the codes must be clearly divisible on decoding, so ambiguous codes such as 1 and 11 could not be used because
11 could be two 1's! The result is that most of the data is compressed considerably (8->1 maximum) and the least frequent values
are actually made bigger as they use very long codes (more than 8 bits are needed due to the decoding problem). Typical Huffman
codes may look like this: 1, 00, 011, 0100, 01010, 01011, .... etc

One fundamental property of images is that each pel is usually similar to its neighbours, so it is usually possible to predict what it will be from previous pels. The difference between the real value and the prediction is usually very small and its statistics are so peaked that compression is made easier.

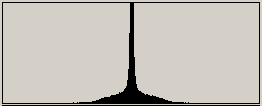
This figure shows a typical histogram of the difference between the previous and current pel (the centre
of the plot is zero) for the text image above. You can see the effect in the difference image intermediate:

Statistical coding such as Huffman, work well with such data. However a difference image actually starts with more values than the original image (-255 to 255 instead of 0 to 255) which could make the compressed data bigger than the original! However a common compression scheme "LZW pel differenced TIFF" actually produces good compression because statistically there are fewer short-codes. Clearly noisy images compress less well. Compressing the full page above makes a 1.9MB file.

LZW is subject to copyright problems now - so the newer deflate algorithm is preferred, but often not supported in things like Photoshop.

By storing the large differences less accurately it is possible to use even fewer bits. This corrupts the image but only where there are big steps, where the eye can not see errors anyway (visual masking occurs). This technique (DPCM: Differential Pulse Code Modulation) can achieve a compression of around 8:1 with little visual effect and is commonly used in broadcasting. Usually a specialised quantiser is used which progressively allocates fewer bits to larger differences.

In summary:
 
 
Original text page 2624 kB 100%
ZIP (deflate) 1754 kB 67%
TIFF LZW 1993 kB 76%
TIFF deflate 1790 kB 68%

JPEG

Designed by the Joint Photograhic Experts Group. This comes under the class of algorithms known as transform coding. These first transform the image into another space, usually similar to the frequency domain, before removing redundancies and coarsely quantizing some elements. So for example an image may be split into 8x8 pel blocks, each is coded separately by transforming into an 8x8 frequency space, then more bits are assigned to some frequencies than others. This is possible since the eye can not easily see errors in the high frequencies for example. For more compression, the higher frequencies can simply be omitted. A statistical technique is then used to compress these codes even more. On decoding the image from the frequency strengths some errors can occur, usually blurring or block effects. The figure below shows the basic frequencies (basis functions) for a 4x4 Hadamard Transform, which uses square waves instead of smooth sine waves. This makes it computationally easier and hence faster but the DCT used in JPEG is now preferred.

You can imagine the DCT basis functions are smoother as they are based on cosines. The top-left function is basically the average of an area, so it is the zero frequency component. The bottom-right represents the highest frequencies. Lower Quality JPEG images assign fewer bits to the higher frequencies.

Although the errors are introduced mainly in the higher frequencies, this means that at lower quality images might not have sufficient high frequancies to "join-up" at the 8x8 block edges. This makes errors like this:


(this has been enlarged 2x by the browser so we can see the pels)

Typical compression ratios below 10X produce "invisible" errors. But if an image is recompressed several times it will become corrupted!
The specific tables of quantisation settings can be tailored to the particular image. This is "adaptive" mode and produces smaller files.

JTIF

JTIF ( JPEG File Interchange Format) is just a file format for a compressed JPEG image. TIFF can actually store its pels compressed in a wider variety of ways, including JPEG. JTIF is the common JPEG file format seen in *.jpg files. SPIFF is an alternative.

JBIG

This is designed to compress 1 bit per pel images like faxes. The standard Group 3 Fax standard suppotred in formats like TIFF work extremely well on one-bit text images.
 

Pyramidal Schemes

Photo CD uses the difference between different resolutions of an image with statistical compression and some small losses. The difference between an image and a version half its size is in fact a range of distinct frequencies in the image. Just as a previous pel difference provides a peaked histogram of values, so does a pyramid of resolutions. One advantage is that lower resolution versions can be extracted without reading all the data. PhotoCD produces high quality images through low compression ratios.

Flashpix - originally a proprietary standard also used a pyramidal scheme.

JPEG 2000

This is a newer system based on Wavelet compression and has extension .jp2. It has the following properties: It is possible to include XML in the file, URLs and other vendor-specific data. The .jpx extension may appear for an extended JPEG2000!
Also the equivalent of MJPEG - MJPEG2000 for movies.
 
 
 

References

JPEG ORG
JJ2000 Java reference implementation
Eusipco2000 documents by Ebrahimi and Cristopoulos.