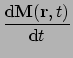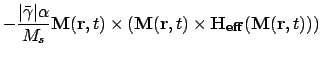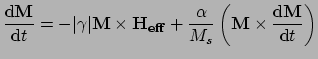


Next: Simulation
Up: Computational models
Previous: The Stoner-Wohlfarth model
Contents
The Landau-Lifshitz-Gilbert equation
With the rapidly-increasing processing capability of modern computers,
there has been a surge of interest in the field of computational
micromagnetics, and indeed computer-based simulation in general. An
important differential equation was derived by Landau and Lifshitz (1935).
The Landau-Lifshitz-Gilbert equation, briefly introduced in
section 2.5, is a fundamental part of
time-dependent computational micromagnetics. Different arrangements of this equation are used in calculations and
simulations.The OOMMF simulation software (Donahue and Porter, 1999) uses the
Landau and Lifshitz form:
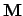 Magnetisation
Magnetisation
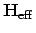 The effective magnetic field, a function of the total energy
The effective magnetic field, a function of the total energy
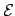
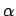 The Landau and Lifshitz phenomenological damping parameter
which is more commonly written as
The Landau and Lifshitz phenomenological damping parameter
which is more commonly written as
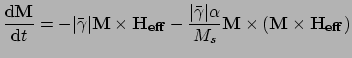 |
|
|
(2.37) |
where
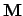 is the magnetisation (i.e. the magnetic
moment per unit volume),
is the magnetisation (i.e. the magnetic
moment per unit volume),
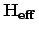 is the effective magnetic
field,
is the effective magnetic
field, 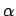 is the Landau and Lifshitz phenomenological damping parameter
(where
is the Landau and Lifshitz phenomenological damping parameter
(where
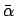 from equation 2.34 is equivalent to
from equation 2.34 is equivalent to
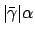 ) and
) and
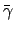 is the Landau and Lifshitz electron gyromagnetic
ratio (the ratio of the magnetic dipole moment to the mechanical
angular momentum of some system). If one assumes
is the Landau and Lifshitz electron gyromagnetic
ratio (the ratio of the magnetic dipole moment to the mechanical
angular momentum of some system). If one assumes
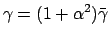 |
|
|
(2.38) |
then this can be shown to be mathematically equivalent to the Gilbert
form (Gilbert, 1955)
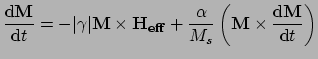 |
|
|
(2.39) |



Next: Simulation
Up: Computational models
Previous: The Stoner-Wohlfarth model
Contents
Richard Boardman
2006-11-28