Alternatively, we can interpret the discrete magnetisation vector
![]() at the surface of the sample as a layer of
dipoles and compute the stray field at the MFM tip and consequently
the second derivative analytically.
at the surface of the sample as a layer of
dipoles and compute the stray field at the MFM tip and consequently
the second derivative analytically.
This approach is more accurate in determining the second derivative
because ![]() in equation 6.6 cannot be made
arbitrarily small. Additionally, an analytical approach is more
flexible with respect to the fly height of the MFM tip.
in equation 6.6 cannot be made
arbitrarily small. Additionally, an analytical approach is more
flexible with respect to the fly height of the MFM tip.
It should be noted that this approach ignores the higher order magnetic moments associated with each simulation cell in OOMMF by replacing them with the leading dipole term. This is justified if the height of the MFM tip above the sample surface is much greater than the OOMMF cell spacing.
![\includegraphics[width=1.0\textwidth]{images/antidots-mfm}](img446.png)
|
The second derivative of the demagnetising energy should be proportional to the signal at the tip of a magnetic force microscope and can be shown (see appendix A) to be:
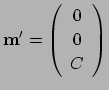 |
(6.8) |
![\includegraphics[width=1.0\textwidth]{images/twofold-realigned-spline-resize-whitespace}](img456.png)
|
Figure 6.9 shows the comparison between the experimental data measured with a magnetic force microscope in zero applied field and the second derivative of the demagnetising field as calculated by the above equation. There is a significant similarity between the images; both show a characteristic periodic parallelogram pattern. The tip distance, both experimental and computed, was half of the distance between the antidot centres.
![\includegraphics[width=1.0\textwidth,clip]{images/antidot-mon-stripes}](img457.png)
|
Figure 6.10 shows a clear agreement between the measurements from the MFM in a small applied field (approximately 10mT) and the computed stray field from the simulation results.
Figures 6.9 and 6.10 suggest that the simulation of a two-dimensional layer with cylindrical holes produces a magnetisation which is at least qualitatively in agreement with the measured magnetisation in the top layer of a three-dimensional sample with spherical holes.