We develop the computational model able to correctly describe the dynamics of multiphase systems with undergoing phase transitions. In particular, we are interested in miscible multiphase flows through porous media.
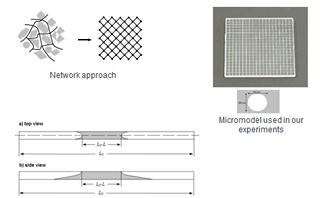
Slowly miscible multiphase systems are ubiquitous in nature and industry. In particular, we are interested in chemical extraction of essential oils from natural feedstock (e.g. production of kitchen vegetable oil), aquifer remediation (cleaning of contaminated soils), and miscible displacements as used for enhanced oil recovery (use of solvents, petrochemical gases or CO2, for displacement/dissolution of oil from the oil reservoir). In all these applications, a porous medium is initially saturated by one liquid, and this liquid is washed out by using a solvent. In porous media, the hydrodynamic flows are rather slow, and diffusive and capillary effects become important. Following a network approach, a porous medium may be represented as the set of capillaries. This helps us to simplify our work by initially adopting the pore-level model.
Thus, to model the miscible multiphase flows through porous media, we need to undertake several steps. First, we need a model that would correctly describe the thermo- and hydro-dynamic evolution of a non-equilibrium binary system. Next, we need to understand the dynamics of the system in a single capillary and then in a network of capillaries. Finally, we need to develop the averaged model capable of describing the miscible multiphase flow through the porous medium at the macro-scale.
The evolution of such a binary mixture is generally defined by the Cahn-Hilliard-Navier-Stokes equations. Nevertheless, such equations are hardly feasible for numerical solution of any practically important problem due to quasi-compressibility that is caused by dependence of mixture density on concentration. By using the multiple-scale method, we filtered out the quasi-acoustic effects and strictly derived the Boussinesq approximation of the Cahn-Hilliard-Navier-Stokes equations. The equations in the Boussinesq approximation define the diffusive and convective dynamics of the miscible multiphase systems.
We have used these equations for investigation of stability of a horizontal miscible interface and for investigation of propagation of gravity capillary waves along a miscible interface.
We also ran the experimental work aimed at understanding the dissolution dynamics from single capillaries and micromodels. The experimental set up was rather straightforward: the capillary or micromodel was saturated with one component of the binary mixture (e.g. glycerol or soybean oil) and was immersed into the solvent(water or hexane)-filled bath. We observed how the solvent diffuses into the tube or micromodel.
Our experimental observations were quite intriguing. A common expectation is that the miscible interface (between glycerol and water or between soybean oil and hexane) within a capillary will not move if there is no externally driven flow; the interface should slowly diffuse owing to interdiffusion of adjoining liquids, and at some point should become invisible. We found that the solvent/solute interface remains visible for rather long time periods. For a capillary, we observed two solvent/solute interfaces propagating into the tube; and for a micromodel, the solute/solvent interfaces propagated from all ends towards the centre. Currently, we are unaware of any theoretical model capable of describing such experimentally-observed dissolution behaviour. This is our primary current research interest.
We are also interested in various complicating factors. Such as, non-isothermal effects, effect of vibrations, etc. In addition, we interested in dynamics of gas/liquid binary systems, such as supercritical CO2/solute mixture.
This work was supported by EPSRC Projects No. EP/G014337 “Pore-level modelling of the miscible displacement”.
Fluid dynamics
Project images:
